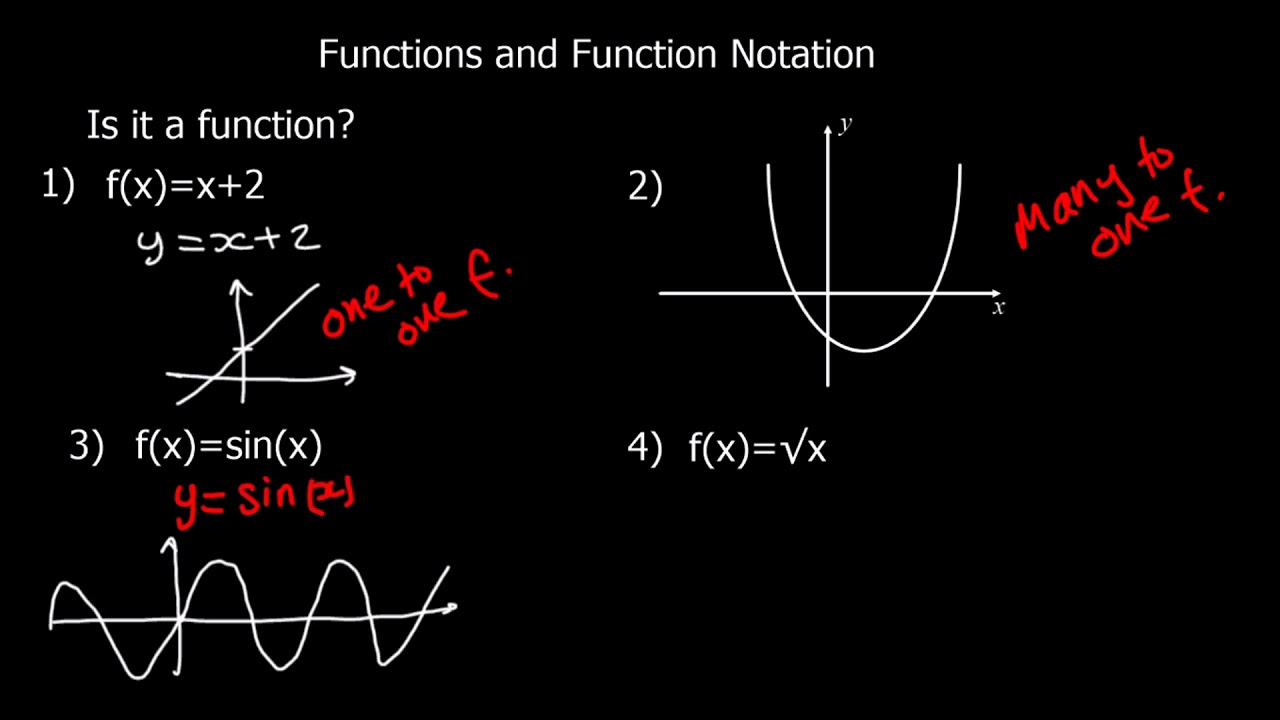
What is a function? A relation between a group of inputs that each have one output is known as a function. To put it simply, a function is a relationship in which each input has a specific relationship to one output. There is a domain, codomain, and range for each function. The general notation for a function is f(x), where x represents the input. A function is generally represented as y = f(x).
What is a Function in Maths?
A Function in Maths is a unique relationship between inputs (also referred to as the domain) and their outputs (also referred to as the codomain) in which each input has one output that can be linked back to its input.
“Book a free Assessment for Maths Tutor“
What is a Function in Algebra?
A function in algebra assigns each input a unique output. It’s a relationship where one variable depends on another.
Example:
The equation f(x)=2x+3 represents a function. For any x, it provides a single, specific f(x).
What is an Inverse Function?
An inverse function reverses the original function’s operation, mapping outputs back to inputs while maintaining a one-to-one correspondence.
Example:
For f(x) = 2x+3,
The inverse is f−1(x) = x−3 ÷ 2
If f(4) = 11,
Then f−1(11) = 4
Types of Functions in maths
Following are the types of Function in Maths :
- 1. One to One Function
- 2. Many to One Function
- 3. Onto Function
- 4. One – One and Onto Function
One to One Function
A one to one function is a unique function in which each element of the range is mapped to exactly one element of its domain i.e, the outputs are never repeated.
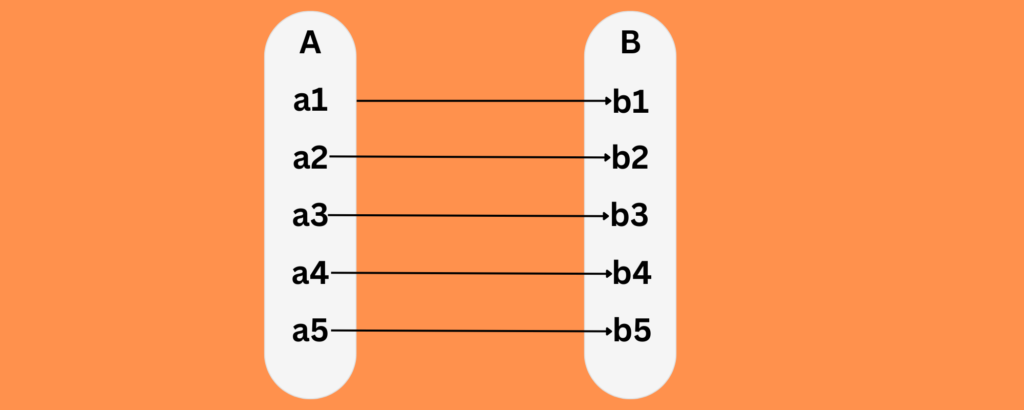
Example
Let’s use the function f(x)=3x−2
Assume f(a1)=f(a2)
So, 3a1−2=3a2−2
Simplify: 3a1−2=3a2−2 which implies 3a1=3a2
Further simplify: a1=a2
Since a1 must equal a2 when f(a1)=f(a2), this function is indeed one-to-one.
- For x=1 : f(1)=3(1)−2=1
- For x=2 : f(2)=3(2)−2=4
- For x=3 : f(3)=3(3)−2=7
X-axis: Represents input values
Y-axis: Represents output values f(x).
Many to One Function
This function transfers one or more elements from set A to an same element in set B. The same image appears in B for two or more of A’s elements.
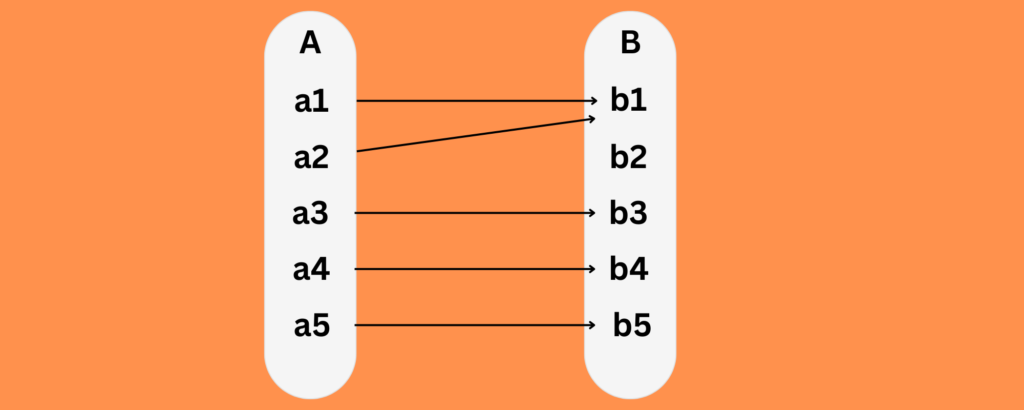
Example
f(x)=x2
x=2 and x=-2
For x=2 ,
f(2)=22=4
For x=−2
f(−2)=(−2)2=4
Onto Function
Onto function could be explained by considering two sets, Set A and Set B, which consist of elements. If for every element of B, there is at least one or more than one element matching with A, then the function is said to be onto function
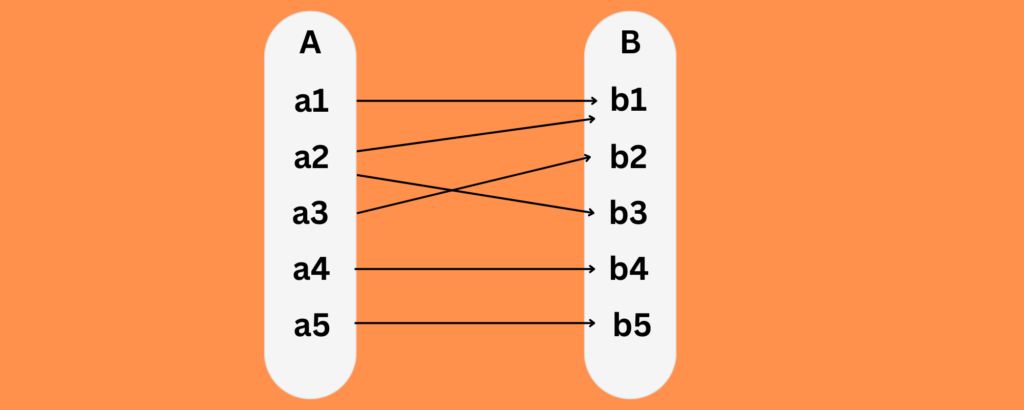
Example
f:R→R
Domain: R (all real numbers)
Codomain: R (all real numbers)
To show that this function is onto, we need to demonstrate that for every y∈Ry \in \mathbb{R}y∈R, there exists an
x∈R such that f(x)=yf(x) = yf(x)=y
Start with f(x)=y
Substitute f(x)with 2x+1
2x+1=y
Solve for x:
2x=y−1
x= y−1 / 2
Since for every y there exists an x (specifically x=y−1 / 2) , f(x)=2x+1 is an onto function.
One – One and Onto Function
Function, f is One – One and Onto or Bijective if the function f is both One to One and Onto function. In other words, the function f associates each element of A with a distinct element of B and every element of B has a pre-image in A.
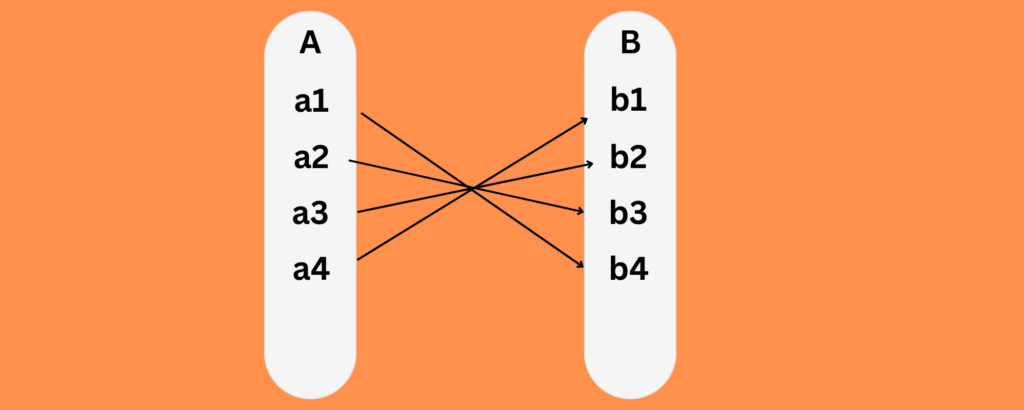
Function: f:{1,2,3}→{a,b,c} defined by:
f(1)=a
f(2)=b
f(3)=c
- Each element of the domain maps to a unique element in the codomain.
- No two domain elements map to the same codomain element.
Conclusion: f is one-to-one.
- Every element in the codomain {a,b,c} is covered.
- a, b, and c are all mapped by 1, 2, and 3, respectively.
Conclusion: f is onto.
Overall: The function f is both one-to-one and onto.
How To Find Minimum or Maximum Value of a function
How To Find Minimum Value of a Function
Given the Function : f(x)=x2−4x+3
- Find the derivative:
f′(x)=2x−4 - Set the derivative equal to zero:
2x−4=0
x=2x - Check the second derivative:
f′′(x)=2
Since the second derivative is positive, the function has a minimum at x=2. - Find the minimum value:
Substitute x=2 back into the original function:
f(2)=(2)2−4(2)+3=1
Thus, the minimum value of the function is 1 at x=2 .
How To Find Maximum Value of a Function
Given the Function : f(x)=−x2+4x+1
- Find the derivative:
f′(x)=−2x+4 - Set the derivative equal to zero:
−2x+4=0
x=2 - Check the second derivative:
f′′(x)=−2
Since the second derivative is negative, the function has a maximum at x=2 - Find the maximum value:
Substitute x=2 back into the original function:
f(2)=−(2)2+4(2)+1=5
Thus, the maximum value of the function is 5 at x=2.
Read More What Is A Range In Math?