Integers are one of the most important number systems in mathematics. They include all positive numbers, negative numbers, and zero.
In this guide, you will learn what integers are, their operations, rules, and key properties. With examples and simple explanations, this blog will help you master integers step by step.
Let’s start with the definition before exploring how integers work.
What Are Integers?
Integers are numbers that include:
- Positive numbers (1, 2, 3…)
- Negative numbers (-1, -2, -3…)
- Zero (0)
They do not include fractions, decimals, or imaginary numbers.
"Get success in maths with our 1-on-1 online maths tutors."
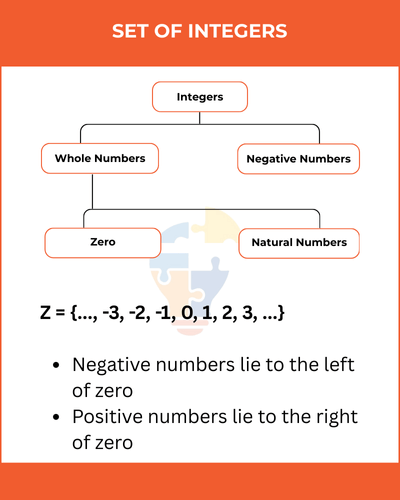
Set of Integers
The set of integers is written as:
Z = {…, -3, -2, -1, 0, 1, 2, 3, …}
Here,
- Negative numbers lie to the left of zero
- Positive numbers lie to the right of zero
Integer Operations
Integers can be added, subtracted, multiplied, and divided just like other numbers.
Addition of Integers
When adding integers:
- If both numbers have the same sign, add their values and keep the sign.
- If they have different signs, subtract the smaller value from the larger and keep the sign of the larger number.
Examples:
- (+5) + (+3) = +8
- (-7) + (-2) = -9
- (-6) + (+4) = -2
Rules of Integers in Addition
- (+) + (+) = Positive
- (-) + (-) = Negative
- (+) + (-) = Depends on the larger number

Subtraction of Integers
When subtracting integers:
- When subtracting integers, turn it into addition and flip the sign of the second number.
Examples:
- 5 − 3 = 2
- 5 − (−3) = 8
- (−7) − (3) = −10
Rules of Integers in Subtraction
- Subtracting a positive → move left on number line
- Subtracting a negative → move right on number line

Multiplication of Integers
When multiplying integers:
- If signs are the same, result is positive
- If signs are different, result is negative
Examples:
- (+4) × (+3) = +12
- (−4) × (−3) = +12
- (+4) × (−3) = −12
Rules of Integers in Multiplication
- (+) × (+) = Positive
- (−) × (−) = Positive
- (+) × (−) = Negative

Division of Integers
When dividing integers:
- If signs are the same, result is positive
- If signs are different, result is negative
Examples:
- (+12) ÷ (+3) = +4
- (−12) ÷ (−3) = +4
- (+12) ÷ (−3) = −4
Rules of Integers in Division
- (+) ÷ (+) = Positive
- (−) ÷ (−) = Positive
- (+) ÷ (−) = Negative

Properties of Integers
Integers follow several important properties that help in solving problems faster.
Closure Property
- Integers are closed under addition, subtraction, and multiplication.
- Example: (−3) + 5 = 2 (still an integer)
Associative Property
- Grouping does not change the result.
- Example: (a + b) + c = a + (b + c)
Commutative Property
- Changing order does not change the result for addition/multiplication.
- Example: a + b = b + a
Distributive Property
- a × (b + c) = ab + ac
Additive Inverse Property
- Every integer has an opposite.
- Example: The additive inverse of +5 is −5.
Multiplicative Inverse Property
- Multiplicative inverse does not exist for all integers except 1 and −1.
- Example: The multiplicative inverse of 1 is 1.
Identity Property
- Additive Identity: a + 0 = a
- Multiplicative Identity: a × 1 = a
Number Line Representation of Integers
A number line is the best way to understand integers:
- Numbers to the right are positive
- Numbers to the left are negative
- Zero is the middle point
Importance of Learning Integers
- Daily Life: Used in temperature (−5°C), bank balance (debt −200), and lifts (floors −1, 0, +1)
- Maths Concepts: Forms the base for algebra and arithmetic
- Science & Data: Used in graphs and data representation
Examples of Integers
- Positive Integers: 3, 9, 12
- Negative Integers: −5, −10, −25
- Zero: 0 (neither positive nor negative)
Tips for Mastering Integers
- Use a number line for practice
- Learn and memorize sign rules
- Practice with real-life examples
Conclusion
Integers are an essential part of mathematics. They include negative numbers, positive numbers, and zero.
Understanding the rules of addition, subtraction, multiplication, and division helps solve problems accurately.
Properties like commutative, associative, and distributive make calculations easier.
By practicing regularly and using number line visualization, students can master integers and build a strong base for algebra and higher mathematics.
Read More What Are Real Numbers? Properties & Examples
FAQs
Q1. What are integers?
Integers are all whole numbers, both positive and negative, including zero.
Q2. Is zero an integer?
Yes, zero is an integer.
Q3. Are fractions integers?
No, fractions and decimals are not integers.
Q4. What is the rule for adding integers?
If signs are same, add values; if different, subtract and keep sign of larger number.
Q5. What is the rule for multiplying integers?
Same signs → positive result; different signs → negative result.
Q6. Can integers be decimals?
No, integers do not include decimals or fractions.
Q7. What is the opposite of +8?
The opposite (additive inverse) is −8.
Q8. Are integers real numbers?
Yes, integers are part of real numbers.
Q9. Where are integers used?
They are used in temperature, bank balance, sports scores, and daily life situations.
Q10. Is −15 an integer?
Yes, −15 is an integer.