Real numbers are the foundation of mathematics. They include almost every number you use daily, from counting objects to measuring distances.
In this guide, we will cover real numbers, their definition, properties, charts, and examples. By the end, you will clearly understand how they work and why they are important in maths.
Let’s dive into the basics and explore real numbers step by step.
Definition of Real Numbers
Real numbers are all the numbers that can be placed on a number line.
They include:
- Natural numbers (1, 2, 3…)
- Whole numbers (0, 1, 2…)
- Integers (-3, -2, -1, 0, 1…)
- Rational numbers (1/2, -4, 0.75)
- Irrational numbers (√2, π, e)
In simple words, real numbers are all numbers except imaginary numbers.
"Get success in maths with our 1-on-1 online maths tutors."
Set of Real Numbers
Real numbers can be divided into two main groups:
- Rational Numbers – Can be written as p/q, where q ≠ 0
- Irrational Numbers – Cannot be written as p/q, decimals never repeat or end
Chart of Real Numbers
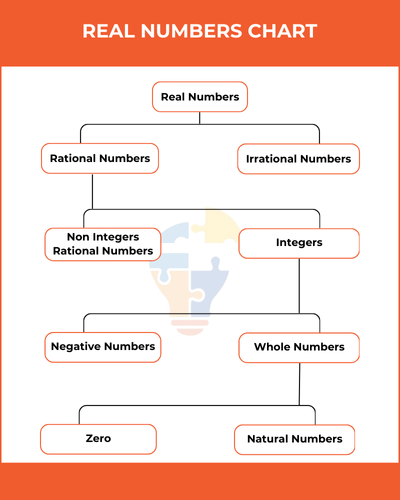
This chart helps visualize how different number types fit under the set of real numbers.
Properties of Real Numbers
Real numbers follow important mathematical properties that make calculations easy.
1. Commutative Property
- Addition: a + b = b + a
- Multiplication: a × b = b × a
- Example: 5 + 3 = 3 + 5
2. Associative Property
- (a + b) + c = a + (b + c)
- (a × b) × c = a × (b × c)
- Example: (2 + 3) + 4 = 2 + (3 + 4)
3. Distributive Property
- a × (b + c) = ab + ac
- Example: 2 × (3 + 4) = 6 + 8 = 14
4. Identity Property
- Additive Identity: a + 0 = a
- Multiplicative Identity: a × 1 = a
5. Closure Property
Real numbers are closed under addition, subtraction, multiplication, and division (except division by 0).

Types of Real Numbers
1. Natural Numbers
Numbers used for counting: 1, 2, 3…
2. Whole Numbers
Natural numbers plus 0: 0, 1, 2…
3. Integers
Whole numbers and their negatives: -2, -1, 0, 1, 2…
4. Rational Numbers
Numbers in p/q form, where q ≠ 0: 1/3, -5, 0.25
5. Irrational Numbers
Numbers that cannot be written as fractions: √3, π
“Book a free assessment for maths tutoring.”
Number Line Representation
Real numbers can be shown on a number line.
- Rational numbers appear as exact points.
- Irrational numbers fill gaps with endless decimals.
This shows that real numbers are continuous and cover the entire line.
Difference Between Real Numbers and Imaginary Numbers
| Feature | Real Numbers | Imaginary Numbers |
|---|---|---|
| Can be Plotted on Number Line | Yes | No |
| Includes Fractions | Yes | No |
| Examples | 2, -3, √5, π | √-1, 3i |
Importance of Real Numbers in Daily Life
- Counting: Money, objects, time
- Measuring: Height, distance, temperature
- Calculating: Business, shopping, science
- Data Handling: Statistics and graphs
Real numbers are everywhere in real life!
Examples of Real Numbers
- Positive Numbers: 1, 3.5, 7
- Negative Numbers: -2, -6.8
- Fractions: 1/2, 3/4
- Irrational: √11, π
Quick Tips to Identify Real Numbers
- If you can place it on a number line → It’s a real number
- If it’s imaginary (√-1), then it’s not real
Conclusion
Real numbers are the most common type of numbers we use. They include natural numbers, integers, fractions, and even irrational numbers like π.
Understanding their properties makes calculations faster and more logical. Real numbers are important in science, engineering, finance, and daily life.
Learning them builds a strong foundation for advanced topics like algebra, calculus, and statistics.
Keep practicing problems and visualizing real numbers on a number line to strengthen your understanding.
Read More What are Irrational Numbers? Properties & Examples
FAQs
Q1. What are real numbers?
Real numbers include natural numbers, whole numbers, integers, rational and irrational numbers.
Q2. Are real numbers and rational numbers the same?
No, rational numbers are a subset of real numbers.
Q3. Can real numbers be negative?
Yes, real numbers include both positive and negative numbers.
Q4. Are fractions real numbers?
Yes, fractions like 1/2 are real numbers.
Q5. Is zero a real number?
Yes, zero is a real number.
Q6. Are irrational numbers real numbers?
Yes, irrational numbers like √2 and π are real.
Q7. Can real numbers be decimals?
Yes, both terminating and non-terminating decimals are real numbers.
Q8. Are all real numbers rational?
No, some real numbers are irrational.
Q9. Is √-4 a real number?
No, it is imaginary.
Q10. Why are real numbers important?
They are used in counting, measuring, and real-life calculations.